Diagrama de temas
-

Análisis Matemático II
Curso 2023
-
-
Guías completas de la materia: link de las guías
-
En este espacio podrán dejarnos sus dudas y consultas acerca del curso.
IMPORTANTE: Les solicitamos que una vez abierto un tema, escriban siempre su consulta en el tópico relacionado.
-
-
- Identificar y graficar las siguientes curvas en \( \mathbb{R}^{2} \):
- \(y=2x^{2}\)
- \(x=y^{2}\)
- \(x^{2}+\frac{y^{2}}{2}=1\)
- \(x^{2}-y^{2}=1\)
- \(y^{2}-x^{2}=1\)
- \(y^{2}+x^{2}=1\)
- \(y^{2}-2x^{2}=1\)
- \(x^{2}-2y^{2}=1\)
- \(\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\)
- \(\frac{x^{2}}{16}+\frac{y^{2}}{25}=1\)
- \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=1\)
- \(\frac{y^{2}}{16}-\frac{x^{2}}{25}=1\)
- \(yx=1\)
- \(y^{2}x^{2}=25\)
- Graficar en \(\mathbb{R}^{3}\) las regiones dadas por las siguientes igualdades o desigualdades:
- \( \left\{ (x,y,z):x=3\right\} \)
- \(\left\{(x,y,z):y<2\right\}\)
- \(\left\{(x,y,z):x=z\right\}\)
- \(\left\{(x,y,z):x+y=4\right\}\)
- \(\left\{(x,y,z):z\leq0\right\}\)
- \(\left\{(x,y,z):xyz=0\right\}\)
- \(\left\{(x,y,z):z+y>3\right\}\)
- Graficar la región de \(\mathbb{R}^{3}\) limitada por el paraboloide \(z=x^{2}+y^{2}\) y el plano \(z=3\).
- Graficar la región de \(\mathbb{R}^{3}\) limitada por los paraboloides \(z=x^{2}+y^{2},\, z=2-x^{2}-y^{2}\).
- Graficar la región de \(\mathbb{R}^{3}\) limitada por las superficies \(z=\sqrt{x^{2}+y^{2}},\, x^{2}+y^{2}=1\) para \(1\leq z\leq2\).
- Graficar los siguientes puntos dados en coordenadas cilíndricas y en cada caso verificarlo calculando las coordenadas rectangulares:
- \((3,\frac{\pi}{2},1)\)
- \((4,\frac{5}{3}\pi,5)\)
- \((3,0,-3)\)
- Graficar los siguientes puntos dados en coordenadas esféricas y en cada caso verificarlo calculando las coordenadas rectangulares:
- \((1,\frac{\pi}{6},\frac{\pi}{6})\)
- \((2,\frac{\pi}{4},\frac{\pi}{3})\)
- \((3,0,\pi)\)
- Para los siguientes puntos dados en coordenadas rectangulares pasarlos a coordenadas esféricas y cilíndricas:
- \((1,1,\sqrt{2})\)
- \((\sqrt{3},0,1)\)
-
- Identificar y graficar las siguientes superficies cilíndricas en \(\mathbb{R}^{3}\):
- \(y^{2}+z^{2}=1\)
- \(y^{2}+4z^{2}=4\)
- \(x-y^{2}=0\)
- \(x^{2}-y^{2}=1\)
- \(z=\cos x\)
- Identificar y graficar las siguientes superficies cuádricas en $\mathbb{R}^{3}\):
- \(4x^{2}+9y^{2}+36z^{2}=36\)
- \(z=x^{2}+y^{2}\)
- \(z=x^{2}-y^{2}\)
- \(16y^{2}=x^{2}+4z^{2}\)
- \(x^{2}-y^{2}+z^{2}=1\)
- \(4z^{2}-x^{2}-y^{2}=1\)
- \(x^{2}-2x+y^{2}-4y+z^{2}=4\)
- Hallar la ecuación en coordenadas rectangulares de las siguientes superficies dadas en coordenadas cilíndricas y luego graficarlas:
- \(r=3\)
- \(z=r^{2}\)
- \(r=4\sin\theta\)
- Hallar la ecuación en coordenadas rectangulares de las siguientes superficies dadas en coordenadas esféricas y luego graficarlas:
- \(\rho=3\)
- \(\rho=2\cos\phi\)
- \(\rho^{2}(\sin^{2}\phi\cos^{2}\theta+\cos^{2}\phi)=4\)
- Escribir las siguientes superficies en coordenadas cilíndricas y esféricas:
- \(x^{2}+y^{2}+z^{2}=16\)
- \(x^{2}+y^{2}=2z\)
- \(x^{2}+y^{2}=2y\)
- \(z=x^{2}-y^{2}\)
- Graficar los sólidos descriptos por las siguientes desigualdades:
- \(r^{2}\le z\le2-r^{2}\)
- \(0\le\theta\le\frac{\pi}{2}\), \(r\le z\le2\)
- \(0\le\phi\le\frac{\pi}{3}\), \(\rho\le2\)
- \(-\frac{\pi}{2}\le\theta\le\frac{\pi}{2}\), \(\frac{\pi}{6}\le\phi\le\frac{\pi}{4}\),
- \(0\le\rho\le4\)
- Dado el sólido comprendido en el interior del cilindro de ecuación \(x^{2}+y^{2}=1\) y entre los planos \(z=0\) y \(z=2\), describirlo en coordenadas cilíndricas.
- Dado el sólido ubicado en el primer octante e interior a la esfera de ecuación \(x^{2}+y^{2}+z^{2}=4\), describirlo en coordenadas esféricas.
- Dado el sólido comprendido en el interior de la esfera \(x^{2}+y^{2}+z^{2}=z\) y en la parte superior del cono \(x^{2}+y^{2}=z^{2}\), describirlo en coordenadas esféricas.
- Graficar las siguientes funciones:
- \(f(x,y)=3\)
- \(f(x,y)=1-x-y\)
- \(f(x,y)=x^{2}+9y^{2}\)
- \(f(x,y)=x\)
- \(f(x,y)=\sqrt{x^{2}+y^{2}}\)
- \(f(x,y)=\sin y\)
- \(f(x,y)=3-x^{2}-y^{2}\)
- En los siguientes casos bosquejar un mapa de nivel considerando varias curvas de nivel:
- \(f(x,y)=\frac{x}{y}\)
- \(f(x,y)=x^{2}-y^{2}\)
- \(f(x,y)=\frac{x+y}{x-y}\)
- Supongamos que tenemos una placa delgada de metal localizada en el plano \(xy\), entonces \(T(x,y)\) es la temperatura en el punto \((x,y)\). Las curvas de nivel \(T\) son llamadas isotermas, pues en todos sus puntos la temperatura es la misma. Bosquejar algunas isotermas si la temperatura esta dada por: \[T(x,y)=\frac{1}{1+x^{2}+2y^{2}}.\]
- En los siguientes casos comprobar que el límite no existe:
- \(\lim_{(x,y)\rightarrow(0,0)}\dfrac{2xy}{x^{2}+2y^{2}}\)
- \(\lim_{(x,y)\rightarrow(0,0)}\dfrac{8x^{2}y^{2}}{x^{4}+y^{4}}\)
- En los siguientes casos comprobar que el límite no existe o demostrar que existe en el punto indicado:
- \(\lim_{(x,y)\rightarrow(1,2)}\dfrac{3-x+y}{4+x-2y}\)
- \(\lim_{(x,y)\rightarrow(4,\pi)}x^{2}\sin(\dfrac{y}{x})\)
- \(\lim_{(x,y)\rightarrow(0,0)}\dfrac{x^{2}y^{2}}{x^{4}+y^{4}}\)
- \(\lim_{(x,y)\rightarrow(0,1)}\dfrac{x}{2x+y}\)
- \(\lim_{(x,y)\rightarrow(0,0)}\dfrac{x^{2}-y^{2}}{x^{2}+y^{2}}\)
- \(\lim_{(x,y)\rightarrow(0,0)\sqrt{\mid x^{2}-y^{2}\mid}}\)
- Dada la función \(f:\mathbb{R}^{2}\rightarrow\mathbb{R}:f(x,y)=\frac{(y^{2}-x)^{2}}{x^{2}+y^{4}}\) si \((x,y)\ne0\), mostrar que para cualquier \(v\ne0,\,\lim_{t\rightarrow o}f(tv)=1\). Ver que no existe \(\lim_{(x,y)\rightarrow(0,0)}f(x,y)\) evaluando la función sobre una curva conveniente.
-
- Hallar las derivadas parciales de las siguientes funciones para cualquier punto del dominio indicado.
- \(f(x,y)=x^{3}+y^{3}-3xy, \, D=\mathbb{R}^{2}\).
- \(f(x,y)=xe^{3y}, \, D=\mathbb{R}^{2}\).
- \(f(u,v)=\arctan{\frac{u}{v}}\).
- \(f(x,y)=\frac{x-y}{x+y}, \,D=\mathbb{R}^{2}-\{(x,y)/x=-y\}\).
- \(f(x,y)=(x^{2}-y^{2})^{\frac{1}{2}},\, D=\mathbb{R}^{2}-\{(x,y)/|x|>|y|\}\).
- \(f(x,y,z)=z^{xy},\,D=\{(x,y,z)/z>0\}\).
- \(f(x,y)=\ln(x+\sqrt{x^{2}+y^{2}})\).
- \(f(x,y,z)=\cos(xyz),\,D=\mathbb{R}^{3}\).
- \(f(x,y,z)=x^{2}e^{yz}\).
- Calcular las derivadas parciales indicadas:
- \(f(x,y)=\sqrt{x^{2}+y^{2}};\,f_{x}(3,4)\).
- \(f(x,y)=\sin({2x+3y}); \,f_{y}(-6,4)\).
- \(f(x,y,z)=\frac{x}{y+z}; \,f_{z}(3,2,1)\).
- \(f(u,v,w)=w\tan(uv); \,f_{v}(2,0,3)\).
- En los siguientes casos calcular todas las derivadas parciales de segundo orden:
- \(f(x,y)=x^{4}-3x^{2}y^{3}\)
- \(f(t,s)=e^{-s}\sin t\)
- \(f(x,y,z)=\frac{x}{x+y+z}\)
- \(f(u,v)=v\tan(2u)\)
- En los siguientes casos verificar que se satisface el teorema de Schwartz \((u_{xy}=u_{yx})\):
- \(u(x,y)=x^{5}y^{4}-3x^{2}y^{3}+2x^{2}\).
- \(u(x,y)=\ln\sqrt{3x-y}\).
-
-
- Usar diferenciación implícita para calcular \(\frac{\partial z}{\partial x}\) y \(\frac{\partial z}{\partial y}\):
- \(xy+yz=xz\)
- \(x^{2}+y^{2}-z^{2}=2x(x+z)\)
- \(xyz=\cos(x+y+z)\)
- Usar la regla de la cadena para calcular \(\frac{dz}{dt}\) en los siguientes casos:
- \(z=yx^{2}+xy^{2},x=2+t^{4},y=1-t^{3}\),
- \(z=\sin x\cos y,x=\pi t,y=\sqrt{t}\),
- \(z=xe^{\frac{y}{w}},x=t^{2},y=1-t,w=1+2t\),
- \(z=xy+yw^{2},x=e^{t},y=e^{t}\sin t,w=e^{t}\cos t\).
- Usar la regla de la cadena para calcular \(\frac{\partial z}{\partial s}\) y \(\frac{\partial z}{\partial t}\):
- \(z=x^{2}+xy+y^{2},x=s+t,y=st\),
- \(z=\sin x\tan y,x=3s+t,y=s-t\),
- \(z=e^{x\theta},x=s+2t,\theta=\frac{s}{t}\).
}Un tanque de agua de forma cilíndrica como se muestra en la figura se está vaciando con un caudal de 5 litros/min , ¿Cuál es la velocidad con la que está disminuyendo la altura del nivel de agua?
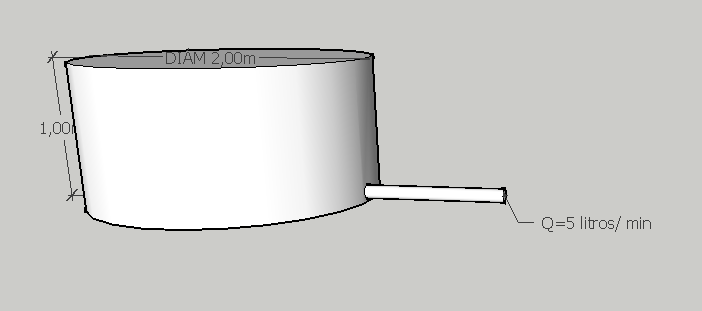
Un tanque de forma cónica como se muestra en la figura se está vaciando con un caudal de 5 litros/min. Se desea saber cuál es la velocidad con la que disminuye el nivel de agua cuando el mismo tiene 1 metro (Volumen del cono truncado \(V=\dfrac{\pi(R^{2}+r^{2}+Rr)h}{3}\).
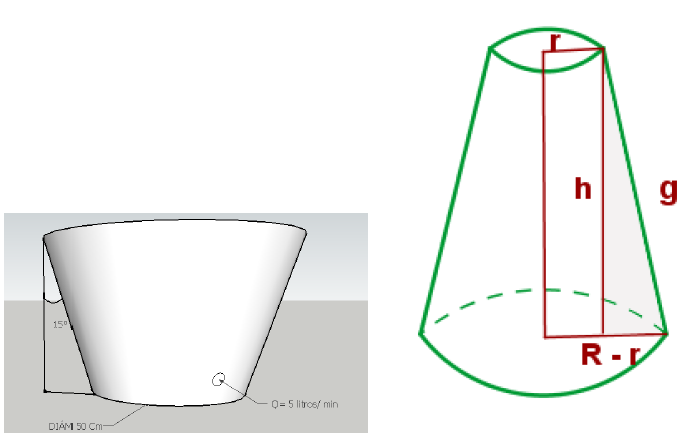
Un tanque de forma esférica como se muestra en la figura se está vaciando con un caudal de 5 litros/ min. Se desea saber cuál es la velocidad con la que disminuye el nivel de agua cuando este es de 1,2 metros. (Volumen de la esfera \(V=\dfrac{4}{3}\pi R^{3}\).
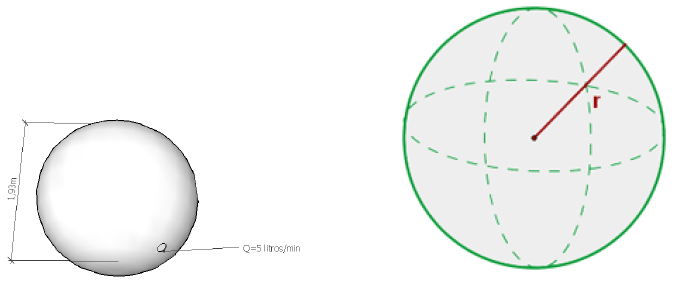
Un tanque de forma cónica (como se muestra en la figura del problema 5) se está vaciando con un caudal que es función de la altura de nivel de agua siguiendo la relación de \(Q=h^{2}\), dada la altura en metros y el caudal (\(Q\)) dado en litros/minuto. Tener en cuenta que existe una evaporación del agua superficial de 1 litro / hora \(m^{2}\). Se desea saber cuál es la velocidad con la que disminuye el nivel de agua cuando éste es de 1,2 metros.
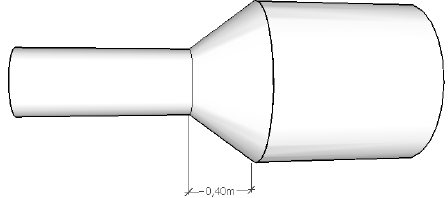
Averiguar la aceleración de una partícula del líquido a la mitad del embudo, sabiendo que el radio mayor es de \(0.5\) m y radio menor es de \(0.2\) m, y posee una longitud de \(0.4\) m. El caudal de entrada y de salida es de \(20\) litros/seg. (Sugerencias: \( a=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dx}{dt};\, v=\frac{Q}{area}=\frac{dx}{dt};\, R(x)=r+(0,4-x)\tan\alpha \).
-
- Calcular, utilizando la definición, la derivada direccional de \(f\) en el punto \(X_{0}\) en la dirección del vector unitario \(u\), en los siguientes casos:
- \(f(x,y)=x-y,X_{0}=(0,0),u=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\).
- \(f(x,y,z)=x^{2}-yz,X_{0}=(1,1,1),u=(1,0,0)\).
- En los siguientes casos, calcular el vector gradiente y evaluarlo en el punto \(P\). Luego, calcular la derivada en el punto \(P\) en la dirección de \(u\).
- \(f(x,y)=x^{3}+y^{3}-3xy,\, P=(2,1),\,u=(1,3)\).
- \(f(x,y)=xy, \,P=(1,3), \,u=(\frac{2}{\sqrt{5}},\frac{-1}{\sqrt{5}})\).
- \(f(x,y)=xe^{xy}, \,P=(1,1), \,u=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\).
- \(f(x,y,z)=ax^{2}+by^{2}+cz^{2}, \,P=(1,0,0), \,u=(0,0,1)\).
- Probar que si \(v\) es un vector de norma \(1\) y \(f\) es diferenciable en \(x_{0}\), entonces \(D_{v}f(x_{0})=\|\nabla f(x_{0})\|cos\theta\), siendo \(\theta\) el ángulo formado por los vectores \(v\) y \(\nabla f(x_{0})\) (recordar que \(\frac{xy}{\|x\|\|y\|}=\cos\theta\), con \(\theta\) el ángulo formado entre los vectores \(x\) e \(y\)). Probar que \(D_{v}f(x_{0})\) es máxima cuando \(v=\frac{\nabla f(x_{0})}{\|\nabla f(x_{0})\|}\).
- Sea \(f:\mathbb{R}^{3}\rightarrow\mathbb{R}\) tal que \(f(x,y,z)=x^{2}-2xy+z^{3}\) y \(x_{0}=(1,-1,2)\). ¿En qué dirección es máxima la derivada direccional? ¿Cuál es ese valor máximo?
- La productividad de una empresa depende del capital invertido y de la cantidad de mano de obra (horas-hombre). Se estableció la siguiente fórmula empírica que describe la situación: \[p(c,h)=8c^{2}-24ch+h^{2}\] Si se lleva invertido \(5000\) y la cantidad actual de horas hombres semanales es de 3000, y tengo cierto dinero disponible, ¿Dónde conviene invertir? ¿En contratar más obreros, o en capital de la empresa?
- Un insecto se halla en un ambiente tóxico. El nivel de toxicidad está dado por: \[T(x,y)=2x^{2}-4y^{2}\] El insecto está en (-1; 2).
- ¿En qué dirección deberá moverse el insecto para que se aleje lo más rápido posible de la toxicidad?
- En la curva de nivel apropiada, ubique y dibuje el vector gradiente en el punto dado.
- ¿Cuál es la razón de cambio de la toxicidad del ambiente en el punto (-1,2) en la dirección (-1,2)?
- La temperatura de cada una de los puntos de una placa cuadrada viene determinada por la función \(T(x,y)=(x-1)^{3}+(y-2)^{2}\) . Se desea conocer cuáles son, en el punto \((0,0)\), las direcciones de mayor crecimiento y decrecimiento de la temperatura.
- La altura de una montaña está dada por la función \(z(x,y)=2e^{-x^{2}}+e^{-3y^{2}}\) ¿En qué dirección desde el punto (1, 0) deberíamos comenzar a caminar para escalar lo más rápido posible?
-
- Encontrar puntos críticos y extremos relativos para:
- \(f(x,y)=x-x^{2}-y^{2} \)
- \(f(x,y)=(x+1)(y-2) \)
- \(f(x,y)=x^{3}+3xy^{2}-15x-12 \)
- \(f(x,y)=e^{x}\cos y \)
- \(f(x,y)=xy(1-x-y) \)
- Encontrar los valores máximos y mínimos absolutos de \(f\) sobre el conjunto \(D\):
- \(f(x,y)=5-3x+4y\), y \(D\) es la región triangular con vértices \((0,0), \,(4,0)\) y \((4,5) \)
- \(f(x,y)=x^{2}+y^{2}+x^{2}y+4\), y \(D=\left\{(x,y):|x|\le1,|y|\le1\right\} \)
- \(f(x,y)=1+xy-x-y\), y \(D\) es la región comprendida entre la parábola \(y=x^{2}\) y la recta \(y=4 \)
- \(f(x,y)=2x^{3}+y^{4}\), y \(D=\left\{(x,y):x^{2}+y^{2}\le1\right\} \)
- Hallar tres números positivos \(x,\,y,\,z\) cuya suma sea \(100\) y su producto \(xyz\) sea máximo.
Un tanque industrial tiene forma cilíndrica con extremos hemisféricos, como se muestra en la figura. El depósito debe almacenar 1000 litros de fluido. Determinar el radio r y longitud h que minimizan la cantidad de material utilizado para la construcción del tanque.

Un edificio rectangular está siendo diseñado para minimizar la pérdida de calor. Las paredes este y oeste pierden calor a razón de 10 unidades/\(m^{2}\) por día, las paredes norte y sur a razón de 8 unidades/\(m^{2}\) por día, el piso a razón de 1 unidad/\(m^{2}\) por día y el techo a 5 unidades/\(m^{2}\) por día. Cada pared debe medir al menos 30 m de largo, la altura debe ser de al menos 4 m y el volumen debe ser exactamente de 4000 \(m^{3}\).
- Encuentre y trace el dominio de la pérdida de calor como función de las longitudes de los lados.
- Encuentre las dimensiones que minimicen la pérdida de calor. (Verifique los puntos críticos y los puntos frontera del dominio)
- ¿Podría diseñar un edificio con incluso menos pérdida de calor, si las restricciones de las longitudes de las paredes se eliminaran?
En una habitación de 10 m de ancho por 8 m de largo se encuentran ubicados dos calefactores: el calefactor 1 de 5000 calorías se encuentra ubicado en el punto \((2,0)\), y el calefactor 2 de 3000 calorías se encuentra ubicado en el punto \((10,3)\). La temperatura en la habitación está dada por la siguiente ecuación:\[T=\dfrac{5000}{d_{1}+1}+\dfrac{3000}{d_{2}+1}\] siendo \(d_{1}\) y \(d_{2}\) las distancias a cada uno de los calefactores (recordar fórmula de distancia \(d=\sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}}\).
- Si me muevo del punto \((8,7)\) en dirección al punto \((3,3)\) con una velocidad de \(2m/s\). ¿Cuál es la velocidad del cambio de T?
- ¿En qué dirección me tengo que mover para que el aumento de T sea máximo?
Encontrar la temperatura máxima y mínima de la habitación.
Un niño se encuentra en una habitación jugando con un globo. En la misma hay un calefactor ubicado en el punto \((8,8,0)\). El volumen del globo cuando el niño se encuentra en el punto \((1,2,5)\) es de 5 \(dm^{3}\). Considerando que
- El volumen del globo está dado por \(V=\dfrac{kmT}{p}\) (\(k,m\) ctes.).
La presión \(p\) está dada por \(p=p_{0}+\dfrac{1}{10}z\), siendo \(p_{0}\) la presión a la altura del piso.
La Temperatura \(T\) está dada por \(T=\dfrac{40}{d^{2}+1}\), siendo \(d\) la distancia al calefactor.
Evaluar como varía el volumen del globo cuando el chico lo desplaza hacia el punto \((3,4,4)\) en un tiempo de 10 segundos y siguiendo una trayectoria rectilínea con velocidad constante. Calcular esa variación en el punto medio de dicha trayectoria. -
- Evaluar las siguientes integrales dobles identificándolas con el volumen de un sólido (no calcular las integrales iteradas
- \(\int\int_{R}3 dA\) siendo \(R=\left\{(x,y):-2\le x\le2,1\le y\le6\right\}\).
- \(\int\int_{R}x dA\) siendo \(R=\left\{(x,y):0\le x\le1,0\le y\le1\right\}\).
- La integral \(\int\int_{R}\sqrt{9-y^{2}}dA,\) donde \(R=[0,4]\times[0,2],\) representa el volumen de un sólido. Graficar dicho sólido.
- Graficar los sólidos cuyos volúmenes están dados por las siguientes integrales:
- \(\int_{-1}^{1}\int_{-1}^{1}\sqrt{4-x^{2}-y^{2}}dydx\)
- \(\int_{0}^{1}\int_{0}^{1}2-x^{2}-y^{2}dydx\)
- Calcular el volumen del sólido que está bajo el plano \(3x+2y+z=12\) y sobre el rectángulo \(R=\left\{(x,y):0\le x\le1,-2\le y\le3\right\}.\) Graficar.
- Calcular el volumen del sólido que está bajo el paraboloide elíptico \(\frac{x^{2}}{2}+\frac{y^{2}}{9}+z=1\) y sobre el rectángulo \(R=[-1,1]\times[-2,2].\) Graficar.
- Calcular el volumen del sólido en el primer octante acotado por el cilindro \(z^{2}=9-y^{2}\) y el plano \(x=2\). Graficar.
- Graficar la región de integración y cambiar el orden de integración para:
- \(\int_{0}^{4}\int_{0}^{\sqrt{x}}f(x,y)dydx\)
- \(\int_{1}^{4}\int_{0}^{\ln y}f(x,y)\,dxdy\)
-
-
- Calcular las siguientes integrales iteradas:
- \(\int_{0}^{a}\int_{0}^{b}\int_{0}^{c}dxdydz\)
- \(\int_{0}^{1}\int_{1}^{2y}\int_{0}^{x}x+2zdzdxdy\)
- \(\int_{0}^{1}\int_{1-x}^{1+x}\int_{0}^{xy}4zdzdydx\)
- Calcular la integral \(\int\int\int_{T}xydV si \(T\) es la región de \(\mathbb{R}^{3}\) limitada por los planos \(x+y+z=1,\,z=0\) e \(y=0\)
- Determinar los extremos de integración para la integral de una función \(f\) sobre la porción del primer octante \(x\ge0,\,y\ge0, \,z\ge0\), cortada por el elipsoide \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1\).
- Calcular el volumen del sólido limitado por el cilindro elíptico \(4=4x^{2}+z^{2}\) y los planos \(y=0\) y \(y=z+2\).
-
- Resolver utilizando coordenadas cilíndricas
- Calcular el volumen del sólido limitado superiormente por el plano \(z-y=0\) e inferiormente por el paraboloide \(z=x^{2}+y^{2}\).
- Calcular el volumen del sólido limitado superiormente por la superficie esférica \(x^{2}+y^{2}+z^{2}=4\), inferiormente por el plano \(xy\) y lateralmente por el cilindro \(x^{2}+y^{2}=1\).
- Resolver utilizando coordenadas esféricas
- Calcular el volumen del sólido comprendido entre el cono \( \varphi=\alpha \) \((\alpha\in(0,\pi))\) y la esfera \(\rho=a\).
- Calcular el volumen común a la esfera \(x^{2}+y^{2}+(z-a)^{2}\le a^{2}\) y al cono \(z\ge\sqrt{x^{2}+y^{2}}\).
- Resolver utilizando las coordenadas que crea más convenientes
- Encontrar el volumen de la porción de la esfera \(x^{2}+y^{2}+z^{2}=a^{2}\), que está dentro del cilindro \(r=a\sin\theta\).
- Considerar el sólido en \(\mathbb{R}^{3}\) limitado superiormente por el cilindro parabólico \(y^{2}+z=4\), inferiormente por el plano \(y+z=2\) y lateralmente por los planos \(x=0\) y \(x=2\). Integrar la función \(f(x,y,z)=y^{2}\) sobre dicha región.
-
- Evaluar las siguientes integrales de línea:
- \(\int_{C}ye^{x}\) \(ds\), donde \(C\) es el segmento que une a los puntos \((1,2)\) y \((4,7)\).
- \(\int_{C}96xy\) \(ds\), donde \(C\) es el arco de curva \(x=y^{4}\) desde \((1,-1)\) hasta \((1,1)\).
- \(\int_{C}z^{2}\) \(ds\), donde \(C\) está formada por los segmentos que unen \((0,0,0)\) con \((2,0,0)\), \((2,0,0)\) con \((1,3,-1)\) y \((1,3,-1)\) con \((1,3,0)\).
Calcular la masa y el centro de masa del siguiente resorte helicoidal considerando: \( (x=\cos4t,y=\sin4t,z=t);0\leq t\leq2\pi, \).
\(\rho=3\)
\(\rho=t^{2}+3\)
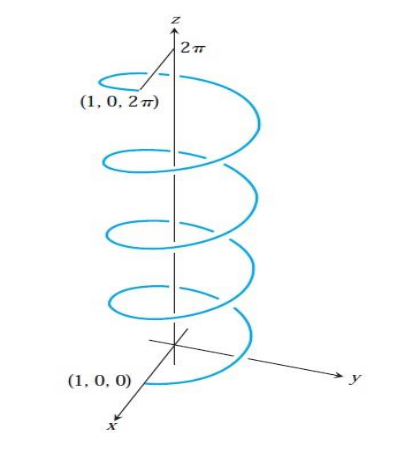
- Calcular el centro de masa del siguiente alambre considerando: \( (x=r\cos\theta,y=r+r\sin\theta);\quad\frac{-\pi}{2}\leq\theta\leq\frac{\pi}{2}, \).
- \(\rho=3\)
\(\rho=1+2\theta\)
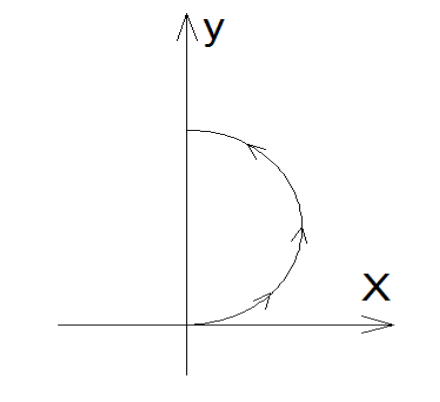
-
Un boomerang está limitado por las siguientes ecuaciones (ver gráfico), y su densidad varía según la función \(\rho=1+2x\), Averiguar:
- masa
- centro de masa
- momento de inercia
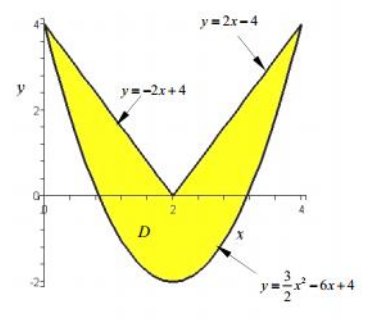
Calcular el área total de la superficie de un granero (techo, paredes, y piso) considerando: Techo: \(z=5-\frac{y^{2}}{5}\) paredes \(x=0\), \(x=4\) piso \(z=0\)

Calcular el centro de masa y momento de inercia de la figura formada por la esfera \(x^{2}+y^{2}+z^{2}=6\) con densidad \(\rho=7\) y el paraboloide a \(z=x^{2}+y^{2}\) , con densidad \(\rho=5\). Considere que el límite entre las distintas densidades es el plano de intersección entre el paraboloide y la esfera.
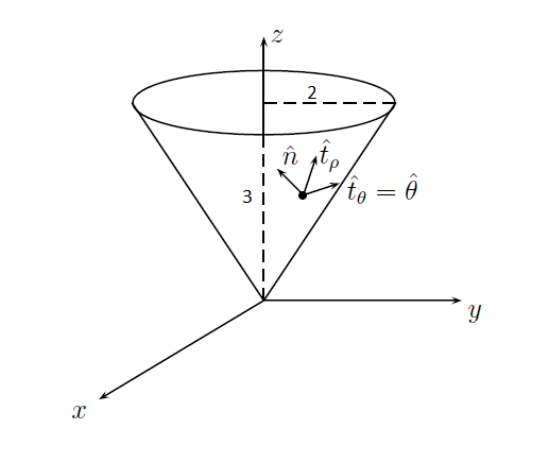
Calcular el área exterior del trompito
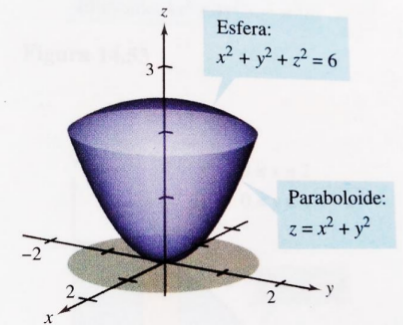
Calcular el centro de masa y centro de flotación para el siguiente barco, sabiendo que la densidad de la parte inferior sigue la fórmula \(\rho=400\) \(kg/m^{3}\) , y la densidad de la parte superior (en gris) es de \(\rho=2000\) \(kg/m^{3}\) . ¿A qué altura respecto al fondo del barco se encuentra la línea de flotación? Considere la densidad del agua como 1000 \(kg/m^{3}\)s
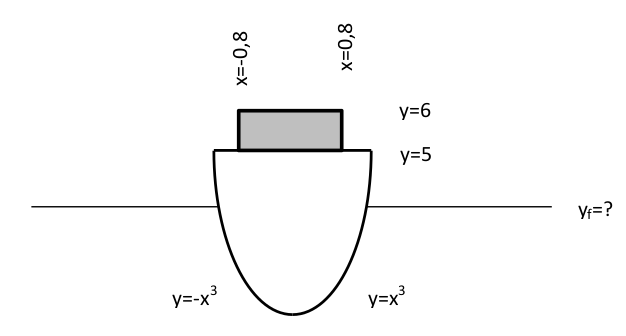
Calcular el área de las siguientes superficies
Región determinada entre el plano \(x+y+z=1\) y el cilindro \( x^{2}+y^{2}=1 \).
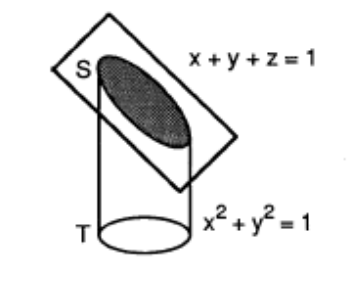
Porción de la esfera \(x^{2}+y^{2}+z^{2}=1\) cortada por el cilindro \(x^{2}+(y-\frac{1}{2})^{2}=\frac{1}{4}\).
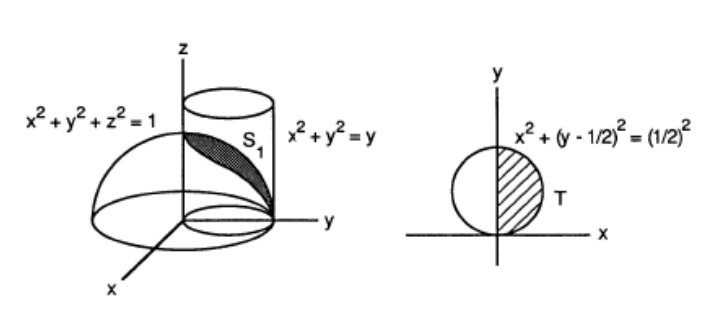
Porción de la esfera \(x^{2}+y^{2}+z^{2}=1\) comprendida entre los planos \(z=\frac{\sqrt{2}}{2}\) y \(z=-\frac{\sqrt{2}}{2}\).
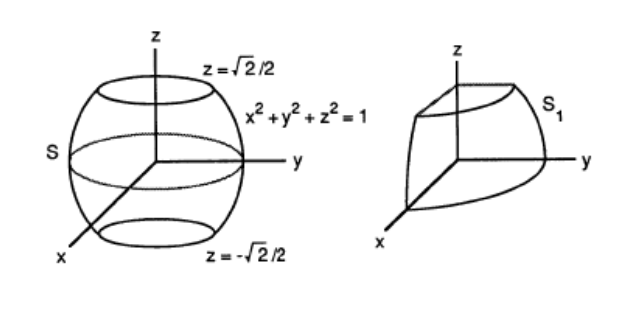
Porción del cilindro \(z^{2}+x^{2}=25\) en el cilindro \(x^{2}+y^{2}=25\).
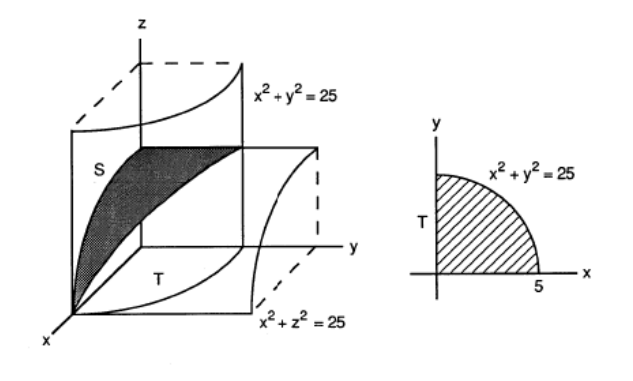
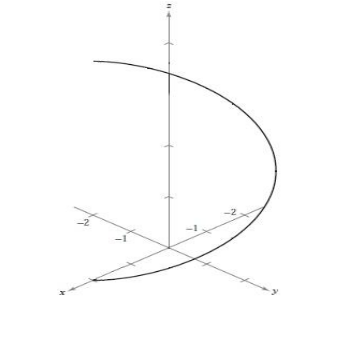
El borde exterior de una escalera de caracol tiene forma de una hélice de 2 metros de radio. La ltura de la escalera es 2 metros y gira tres cuartos de una revolución completa de abajo a arriba.
- Hallar una función vectorial para la hélice.
- Hallar la longitud de la hélice.
-
- Calcular la integral de línea \(\int_{C}F.dr\) sobre la curva indicada:
- \(F(x,y)=(y,x);\Gamma=\{(t,t^{2}):t\in[0,1]\}\).
- \(F(x,y)=(\cos x-y\sin x)e_{1}+(\cos x)e_{2};\) en el triángulo con vértices \((0,2),(2,3)\) y \((1,4)\) recorrida en el sentido inverso a las agujas del reloj.
- \(F(x,y,z)=(x,y,xz-y)\); sobre el segmento que va desde el punto \((0,0,0)\) hasta el punto \((1,2,4)\).
- \(F(x,y,z)=(x^{2},xy,z^{2})\); sobre la curva dada por \(r(t)=(\sin t,\cos t,t^{2})\) con \(t\in[0,1]\).
El campo de fuerzas \(\overrightarrow{F}(x,y)=(x+y)\textbf{i}+x^{2}+1)\textbf{j}\) actúa sobre un objeto que se mueve desde el origen al punto \((0,1)\).
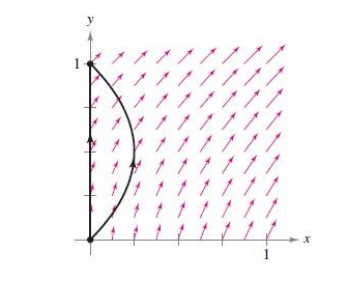
Hallar el trabajo realizado si el objeto sigue la trayectoria \( x=0, \) \(0\leq y\leq1\).
Hallar el trabajo realizado si el objeto sigue la trayectoria
\(x=y-y^{2}\) , \( 0\leq y\leq1\ \).
Supóngase que el objeto sigue la trayectoria \(x=c(y-y^{2})\), \(0\leq y\leq1\) , \(c>0\). Hallar el valor de la constante c que minimiza el trabajo.
Hallar el trabajo realizado por el campo de fuerzas \(F(x,y,z)=(zy,xz,xy)\) para mover una partícula a lo largo de la curva \(r(t)=(t^{2},-t^{3},t^{4})\) desde \(t=0\) a \(t=1\).
-
- La diferencia de potencial \(\Delta V\) entre los puntos A y B en un campo eléctrico \(\overrightarrow{E}\) se define como:\(\Delta V=\int_{A}^{B}\overrightarrow{E}d\overrightarrow{s}\) Dado el campo eléctrico \(\overrightarrow{E}(x,y,z)=5x\textbf{i}+2y\textbf{j}+0\textbf{k}\) \([\frac{N}{C}]\)
- Encuentre la función potencial.
- Utilizando la función encontrada en el ítem anterior, calcular la diferencia de potencial entre los puntos \((1,3,3)\) y \((1,12,7)\).
- Calcule la integral de línea utilizando una trayectoria recta entre los puntos del ítem anterior.
- Recalcule la integral de línea entre los mismos puntos anteriores eligiendo una trayectoria conveniente (ayuda: considere trayectoria paralela a los ejes).
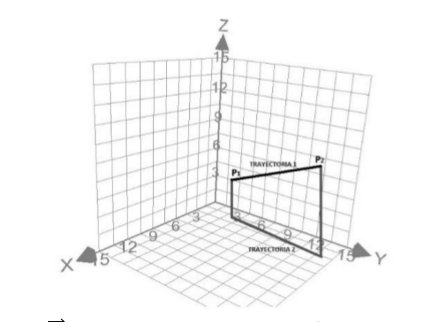
- Para los siguientes incisos:
- \(F(x,y)=(x^{3}y^{4},x^{4}y^{3}),\) \(C(t)=(\sqrt{t},1+t^{3})\)
\(t\in[0,1]\).
\(F(x,y,z)=(y,x+z,y)\), \(C\) es el segmento de recta desde \((2,1,4)\) hasta '\((8,3,-1)\).
Hallar una función \(f\) que verifica \(F=\nabla f\)
Usar el anterior cálculo para evaluar \(\int_{C}F.dr\) a lo largo de la curva \(C\) dada.
Determinar si \(F\) es un campo conservativo. Si lo es, hallar la función potencial \(f\) (i.e. la función que verifica que \(F=\nabla f\)).
- \(F(x,y)=(6x+5y,5x+4y)\).
- \(F(x,y)=(ye^{x}+\sen y,e^{x}+x\cos y)\).
- \(F(x,y)=(xe^{y},ye^{x})\).
-
- Sean \(u,v\) \(:D\subset\mathbb{R}^{3}\rightarrow\mathbb{R}^{3},\alpha\in\mathbb{R}\). Mostrar que:
- \(div(u+v)=div\) \(u+div\) \(v\).
- \(div(\alpha.v)=\alpha.div\) \(v\)
- Si \(f:\mathbb{R}^{3}\rightarrow\mathbb{R}\) es una función escalar y \(v:U\subset\mathbb{R}^{3}\rightarrow\mathbb{R}^{3}\), probar que \(div(f.v)=f.div(v)+\nabla f\cdot v\)
- Se define el Laplaciano de una función escalar \(f\) como \(\nabla^{2}f=\dfrac{\partial^{2}f}{\partial x^{2}}+\dfrac{\partial^{2}f}{\partial y^{2}}+\dfrac{\partial^{2}f}{\partial z^{2}}.\)
- Probar que \(\nabla^{2}f=div(\nabla f).\)
- Probar que \(div(f\nabla f)=f\nabla^{2}f+\Vert\nabla f\Vert^{2}.\)
- Hallar el rotacional de \(v(x,y,z)=xy.e_{1}+xz.e_{2}+z.e_{3}\)
- Sean \(u,v\) \(:D\subset\mathbb{R}^{3}\rightarrow\mathbb{R}^{3},\alpha\in\mathbb{R}\). Mostrar que:
- \(rot(u+v)=rot(u)+rot(v)\).
- \(rot(\alpha.v)=\alpha.rot(v)\)
- Sea \(f:\mathbb{R}^{3}\rightarrow\mathbb{R}\) es una función escalar y \(v:\mathbb{R}^{3}\rightarrow\mathbb{R}^{3}\). Notaremos con \(\nabla f\) al gradiente de la función \(f\). Demostrar que \(rot(fv)=f.rot(v)+\nabla f\times v\)
- Demostrar:
- \(rot(\nabla f)=0\)
- \(div(rot(v))=0\)
- Sea \(v\) un campo en \(\mathbb{R}^{3}\), \(v=(v_{1},v_{2},v_{3})\). Definimos \(\nabla^{2}v=(\nabla^{2}v_{1},\nabla^{2}v_{2},\nabla^{2}v_{3})\). Demostrar que \(rot(rot(v))=\nabla(div(v))-\nabla^{2}v.\)
-
- Calcular utilizando el teorema de Green, donde \(C\) se considera positivamente orientada:
- \(\int_{C}3y\) \(dx+5x\) \(dy\), \(C:x^{2}+y^{2}=1.\)
- \(\int_{C}xy\) \(dx+2x^{2}\) \(dy\), donde \(C\) consiste en el segmento que une los puntos \((-2,0)\) y \((2,0)\) y la parte superior del círculo \(x^{2}+y^{2}=4\).
- \(\int_{C}(e^{x}\sin y)\) \(dx+(e^{x}\cos y)\) \(dy\), \(C:(x-a)^{2}+(y-b)^{2}=r^{2}.\)
- \(\int_{C}F.dr\), donde \(F(x,y)=(y^{2},x^{2})\) y \(C\) es el segmento que une los puntos del \((1,1)\) al \((0,0)\) seguido del arco de la parábola \(y=x^{2}\) desde \((0,0)\) al \((1,1)\).
- \(\int_{C}F.dr\), donde \(F(x,y)=(y^{2}-x^{2}y,xy^{2})\) y \(C\) consiste en el círculo \(x^{2}+y^{2}=4\) desde \((2,0)\) al \((\sqrt{2},\sqrt{2})\) y los segmentos de recta desde el \((\sqrt{2},\sqrt{2})\) al \((0,0)\) y desde el \((0,0)\) al \((2,0)\).
- Verificar el teorema de Green, donde $C$ se considera positivamente orientada:
- \(\int_{C}x^{5}y^{4}\) \(dx-x^{4}y^{5}\) \(dy\), \(C:x^{2}+y^{2}=1.\)
- \(\int_{C}x\) \(dx+x^{3}\) \(dy\), donde \(C\) consiste en el segmento que une los puntos \((-3,0)\) y \((3,0)\) y la parte inferior del círculo \(x^{2}+y^{2}=9\).
- Comprobar el teorema de Stokes sobre el triángulo de vértices \( (2,0,0);(0,2,0);(0,0,2) \) para:
- \(v(x,y,z)=2z.e_{1}-y.e_{2}+x.e_{3}\).
- \(v(x,y,z)=z^{2}.e_{1}-4x.e_{2}+y^{3}.e_{3}\).
- En los siguientes casos utilizar el teorema de Stokes para calcular \(\iint_{S}rot\) \(F.ds\).
- \(F(x,y,z)=yz\) \(\textbf{i}+xz\) \(\textbf{j}+xy\) \(\textbf{k}\) y \(S\) es la parte del paraboloide \(z=9-x^{2}-y^{2}\) que está por encima del plano \(z=5\).
- \(F(x,y,z)=x\) \(\textbf{i}+y^{2}z\) \(\textbf{j}+z\) \(\textbf{k}\) y \(S\) es la parte de la semiesfera \(x=\sqrt{9-y^{2}-z^{2}}\) que está dentro del cilindro \(y^{2}+z^{2}=4\).
- Verificar el teorema de Stokes en los siguientes casos:
- Sobre la mitad superior de la esfera unidad \(x^{2}+y^{2}+z^{2}=1\) para \(v(x,y,z)=x.e_{1}+y.e_{2}+z.e_{3}\)
- Sobre el cuadrado de vértices \((0,0,0)\), \((1,1,0)\), \((0,0,\sqrt{2})\) y \((1,1,\sqrt{2})\) y el campo vectorial \(F(x,y,z)=(ze^{-y},z,y)\).
- Utilizar el teorema de Stokes para evaluar \(\int_{C}F.dr\) donde \(F(x,y,z)=(x^{2}z,xy^{2},z^{2})\) y \(C\) es la curva de intersección del plano \(x+y+z=1\) con el cilindro \(x^{2}+y^{2}=9\) orientado en sentido contrario a las agujas del reloj visto desde arriba.
- Verificar el teorema de Stokes para el campo vectorial dado por \(F(x,y,z)=(y+z)\textbf{i}+(x^{2}+z^{2})\textbf{j}+y\textbf{k}\) y para la superficie \(S=\{(x,y,z):x^{2}+z^{2}=4,z\leq0,0\leq y\leq3\}\).
- Utilizar el teorema de la divergencia para evaluar la integral de superficie \(\iint_{\partial W}F.ds\) donde \(W\) es la bola maciza definida por \(x^{2}+y^{2}+z^{2}\leq1\) en los siguientes casos:
- Cuando \(F(x,y,z)=2x\textbf{i}+y^{2}\textbf{j}+z^{2}\textbf{k}\).
- Cuando \(F(x,y,z)=(x,1,1)\).
- Comprobar el teorema de la divergencia para el caso en que \( F(x,y,z)=(xy^{2},x^{2}y,y) \) y \(S\) es la superficie que bordea al sólido comprendido entre el cilindro \(x^{2}+y^{2}=1\) y los planos \(z=-1\) y \(z=1\).
- Comprobar el teorema de la divergencia en los siguientes casos:
- Sobre la bola unidad \(x^{2}+y^{2}+z^{2}\leq1\) para el campo vectorial \(v(x,y,z)=x.e_{1}+y.e_{2}+z.e_{3}\).
- Sobre la parte del cono \(x^{2}+y^{2}=z^{2}\) que se halla entre los planos \(z=1\) y \(z=4\) para el campo \(F(x,y,z)=(x^{2},y^{2},z^{2}).\)
- Calcular el flujo saliente del campo \(F=-3\textbf{k}\) a través de la superficie del cono invertido (sólo a través de la parte cónica), usando el teorema conveniente.
 Bibliografía:
Bibliografía: